什么叫做计数单位和数位（数与代数之数位）

一．概念描述

现代数学：数位是命数法术语，指各个不同的记数单位所占的位置。即在记数时，按照一定的顺序把各个数字排列在固定的位置上，一个数字占有一个位置，以区别它们的单位，这些位置都称为数位。相对来说，左边的数位高于右边的数位。

例如，在十进制记数中，六万一千三百七十五记为：6 1 3 7 5

万 千 百 十 个

位 往 往 位 住

这是一个五位数，每个数字各占一个数位，其中十位对个位来说是高位，对百位来说，它又是低位。

小学数学：小学数学教材并没有给出数位的明确概念，只是通过提问的方式请学生填出从右边起，第一位是个位，第二位是十位，第三位是百位。

二．概念解读

(1)数位与数位顺序

数位顺序表给出了数位顺序的分类法则，即按照由小到大的顺序把记数单位从左到右排成表格。我国常用的整数数位顺序表为：

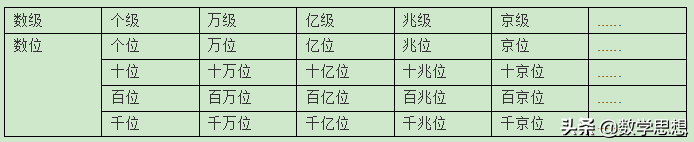
表中数级名和数位是按照目前我国四位分级的读数和记数习惯列出的，而目前国际通用的读数和记数法是三位分节制，国际整数数位顺序表为：

对于百密位( 100 000 000)以上的高单位数的命名习惯，美国与英国是有差别的。如对10⁹，美国称为别位，英国称为千密位。

(2)数位与计数单位

每一个计数单位都与相应数位一一对应，协同完成计数任务。数位决定着计数单位的大小，计数单位为数位计数服务。比如，36的3在十位上，表示3个十，6在个位上，表示6个一......它们存在密切关系。

(3) 数位与位数

“数位”是指一个数的每个数字所占据的位置。例如，621中有三个数字，它们所占的位置分别是百位、十位和个位。这里的百位、十位和个位就是这个数所占的数位。“位数”是指一个数所占数位的个数。如621占据了百位、十位和个位三个数位，我们就说它是一个三位数。

三．教学建议

(1)在富有挑战性的数学活动中发展学生数感

“数与代数”学习的核心目标是使学生在数感、符号意识、运算能力等多方面获得发展。而发展数感作为数学学习的核心目标，它需要贯穿在具体的数学教学过程中，需要教师精心设计数学活动，为学生的数感发展提供条件。张丹老师曾执教“认识百及百以内的数”一课，其中进行了四次的“数一数”活动可谓亮点。

初数百以内的数，了解学生已有的数数经验。这就是要让学生借助自己已有的数数经验，初步感知百及百以内的数。此时，张老师为学生提供了数量不同的学具，有芸豆、小正方体、小棒、铅笔等。

再数百以内的数，感受按群计数和数数策略的多样化。当发现学生数数的方法仅仅停留在“1个1个”地数，而且数过之后仍把学具堆成一堆，也就是数数经验和方法没有发展时，张老师又提出了一个具有挑战性的问题：能不能想个好方法，让别人一看就知道是多少？这时学生思维从“无疑”到“有疑”，冲突出现了。在智慧碰撞中，多种数数的方法和策略也随之出现了。

三数百以内的数，感受数之间的联系。当学生数出自己的学具不够100或比100多时，张老师继续追问：怎样才能得到100个？学生在说出不够100再加几个、比100多几个就得去掉几个时，不仅感受到了百以内数之间的联系，而且体验了递加和递减的过程，同时巧妙地建立了“百”这个数位。可见，每个活动都富有目的、具有挑战性，学生的数感正是在挑战性的活动中逐渐得以发展的。

四数百以内的数，体会数位与计数单位间一一对应的关系。

(2)在比较数的大小中突出“数位”概念本质的教学

数的大小比较是一个重要的学习内容。有关数的大小关系主要包括数的相等、大于、小于的意义及符号表示，大小比较的方法，大小比较的应用，以及在具体情境中把握数的相对大小关系。

有关数的大小比较方法，教师应鼓励学生自主探索。有的学生可能会采用“数数”的方法，即“后数的数就大”。于是，只要他会数数，就会比较大小，而实际上他是借助了“顺序”来比较大小的。当然，也有的学生会逐渐认识到没有必要一个一个地对应，也可以一个一个计数单位对应，从而探索出“常规方法”。作为教师，不仅要了解这些方法间的联系，还要适时为学生展示这种联系。在小学阶段学习的自然数大小比较、小数大小比较的法则看起来是位数、数位间的比较，但实质却是计数单位及其个数的比较。就像自然数、小数加减法计算一样，表面看是相同数位对齐，同—数位上的数相加减，实质上是相同计数单位相加减。