渐近线方程公式（指数函数有渐近线？）

一起来看道题：

本题首先画出函数f(x)的草图。

一步一步来，先画出函数y=3^x的草图，这是常见的指数函数，而且底数3>1，所以在R上为单调递增函数。

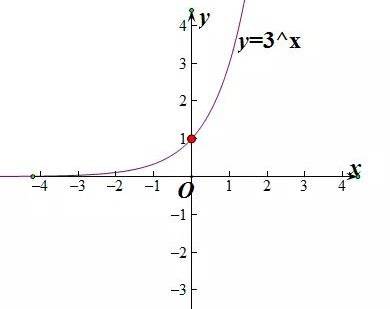
然后画出函数y=3^x-1的草图，只需把上面这个函数的图象向下平移1个单位长度即可。

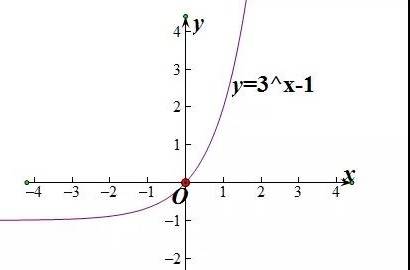
接下来画出函数y=|3^x-1|的草图。同学们都学过图象的绝对值变换规律，只需把上面这个函数的图象在x轴上方的部分保留，在x轴下方的部分沿x轴翻折上去即可。

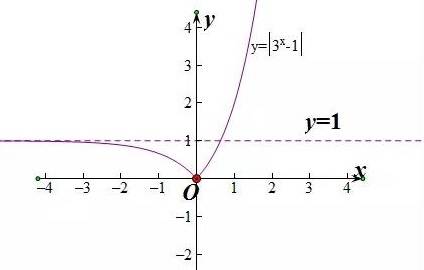
请注意画图的准确性。

考试时虽然画的是草图，不可能太准确，但是关键的位置必须画对。

渐近线！

函数y=3^x的图象有一条渐近线是y=0，则函数y=3^x-1的图象有一条渐近线是y=-1。此函数图象x轴下方的部分翻折上去之后，得到函数f(x)=|3^x-1|的图象，则新函数图象有渐近线y=1，如上图所示。

由函数f(x)的图象可以看出，f(x)有两个单调区间，在负区间为单调减函数，在正区间为单调增函数。

那么三个自变量a,b,c分别应该在什么范围之内呢？

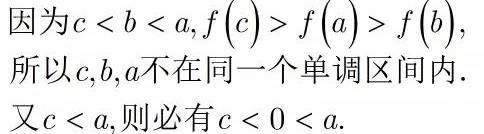
可是b在什么范围内呢？

从已有的条件来看，b介于c，a之间，但是我们无法确定b>0还是b<0.结合函数值的大小关系，可能的图形如下。

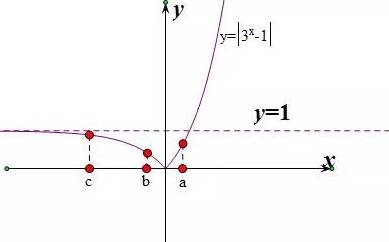
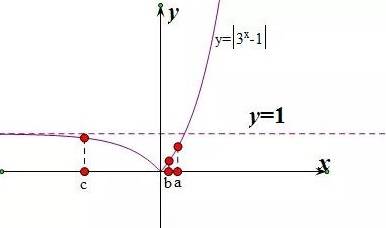
因为b是否大于0不确定，所以3^b是否大于1就不确定，故不能选A和B。

再来研究选项C和D。

假设在正区间存在点c'，使得f(c')=f(c)，如下图所示。

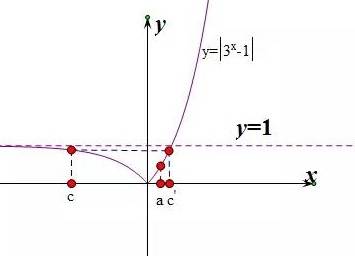
由图可知c'>a>0。

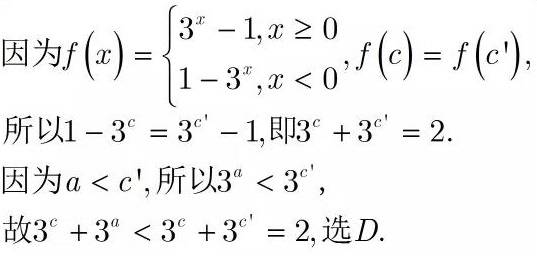
对于绝对值函数，通过作一条平行于x轴的平行线找到与f(c)相等的另外一个位置，是解决这类问题的常用做法。