阿贝尔求和公式 ,发明了一种新的数值方法,可以计算最神秘的常数欧拉常数
数学在某些方面与科学一样是艺术和创造力。欧拉在复数被理解之前取负数的平方根,拉马努詹研究的发散级数对当时的数学家来说没有任何数学意义,但这些结果在100多年后被应用于量子力学和弦理论。
我的观点是,有时候以一种非正式的方式来“玩”数学是可以的。当然,最终,我们需要一个有效的、一致的理论,并对定理进行严格的证明。在这篇文章中,我将给你们一些有趣的想法,这个理论实际上是一致的,更重要的是,我们可以把它应用到实际问题中。
底函数和分数函数
在解析数论中,级数和积分通常涉及到底函数所以它的定义如下:
另一个非常常用的函数是分数部分函数。x的小数部分表示为{x},定义为{x} = x - [x]。例如{3.2}= 0.2,{2/3}= 2/3。
注意,这些函数不是连续的。底函数的曲线图如下:
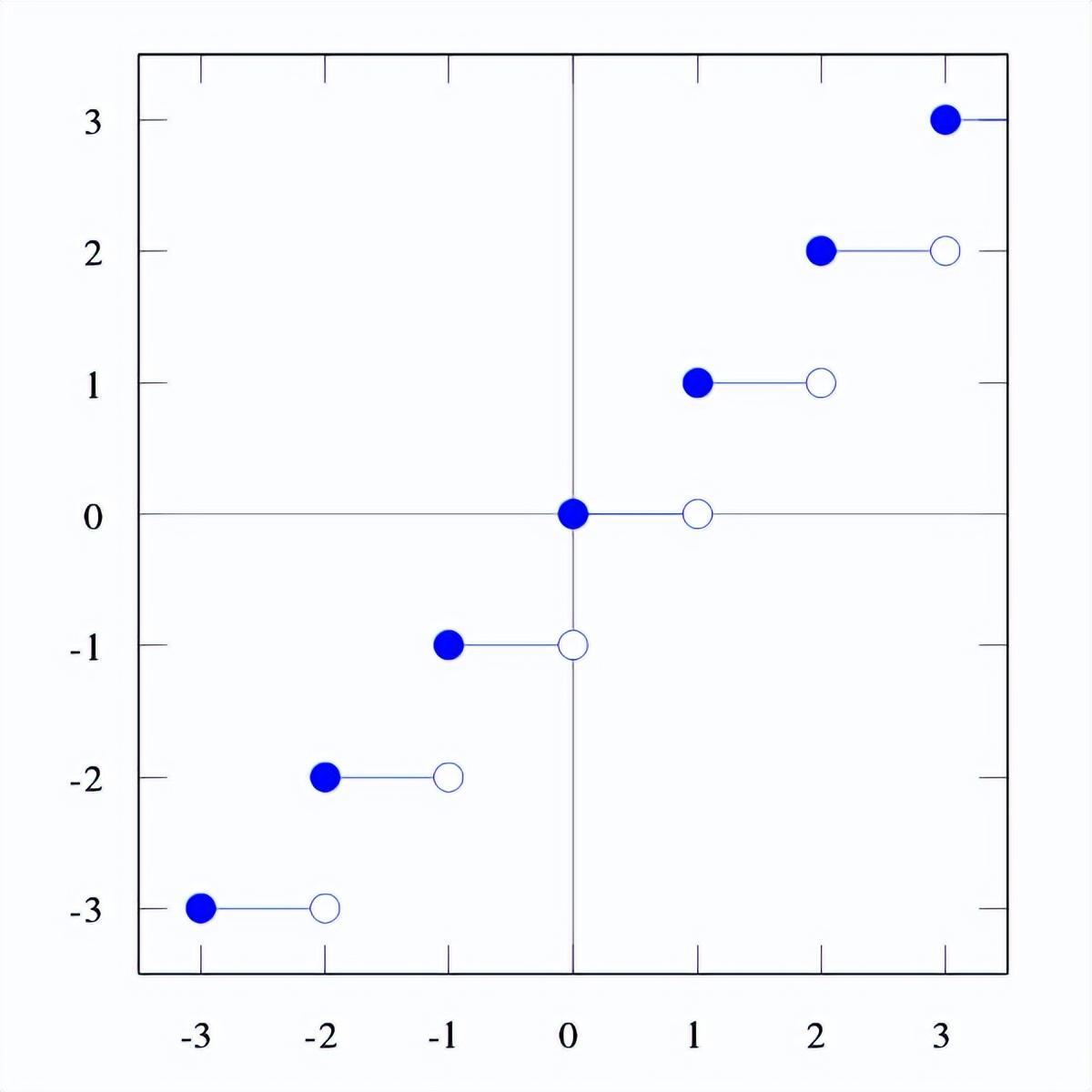
正如你所看到的,底函数的图形在整数值处有“跳跃”,使其在这些值处不连续。
分数部分函数的图如下:
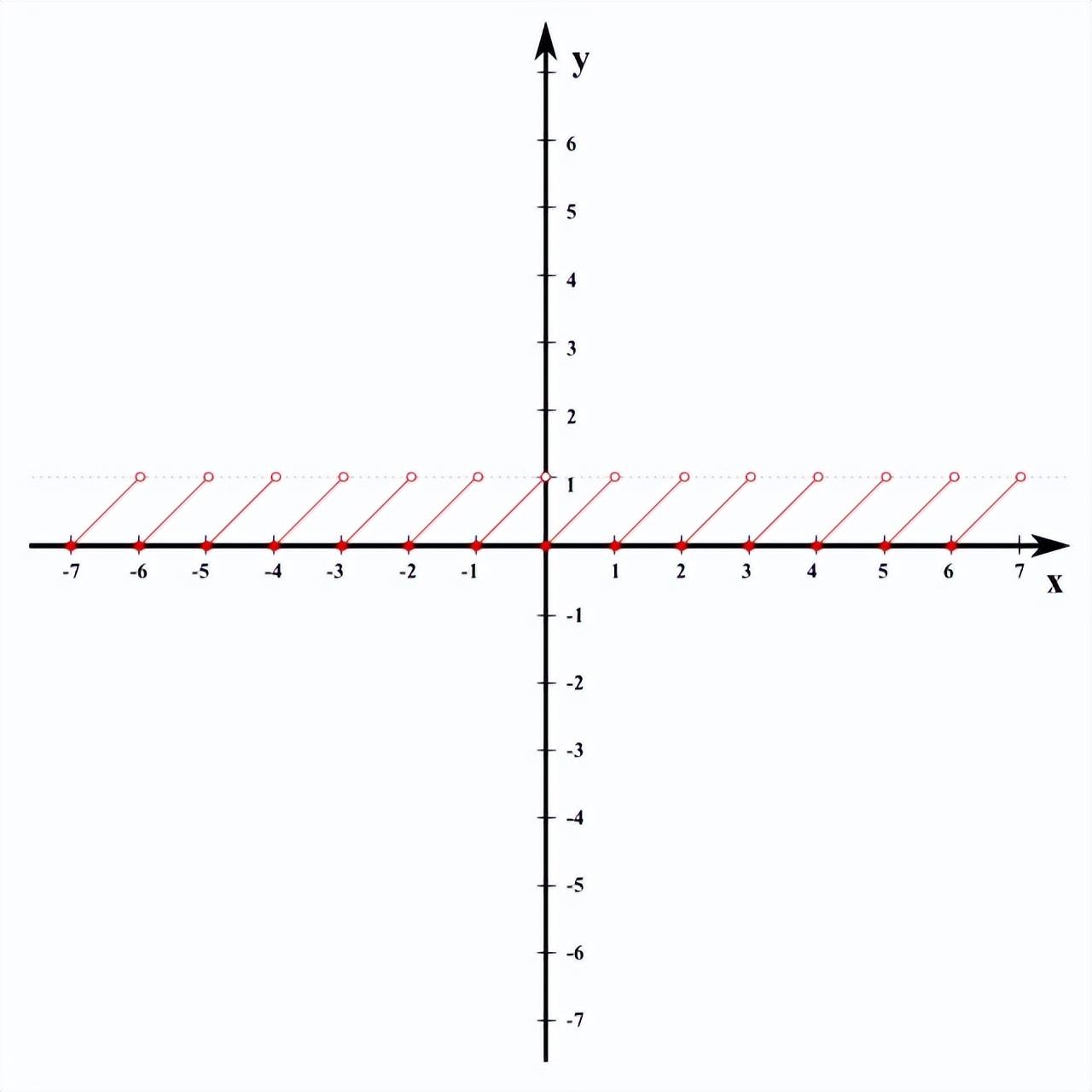
这个图在整数处有“跳跃”,但如果你把这两个图加在一起,你几乎可以看到底函数的跳跃是如何被小数部分填满的,从而得到恒等函数f(x) = x。
数论的应用
之前我说过这些函数在数论领域中被大量使用,但是具体在哪被使用,以及为什么?其中之一是一个著名的结果,阿贝尔求和。
设x > 1为实数,且实函数f可微,则下式成立:
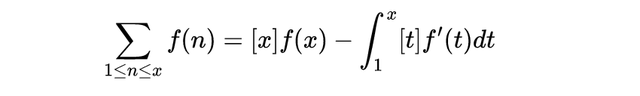
和是1和x之间的所有自然数的和。
建议读者自己去证明这个结果,不过这里有个小的提示:
你可以用很多方法证明这个结果,实际上这是一个更一般的定理的特殊情况,但在这篇文章中,我们只需要上面的结果。
这个公式把和式转换成积分,反之亦然,让我们试着把它应用到一个非常有趣的和式上,也就是调和级数。换句话说,让f(t) = 1/t,我们把阿贝尔求和公式应用到这个函数上。
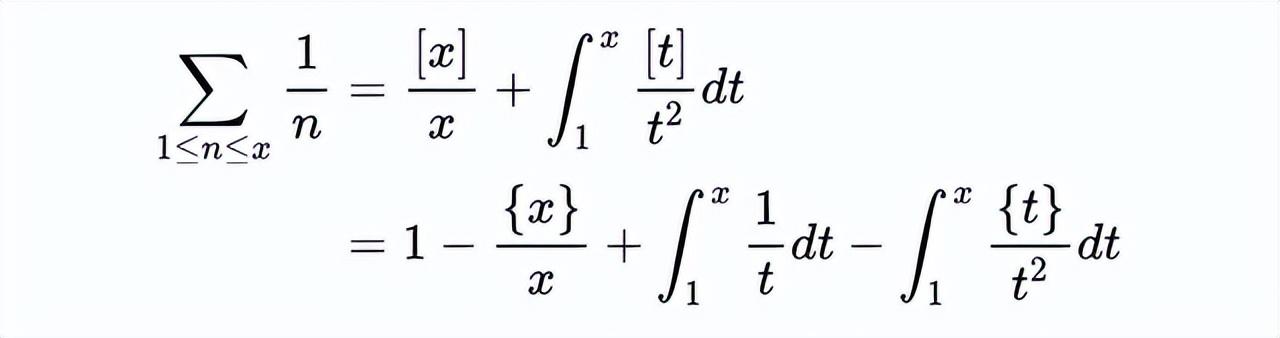
我们用小数部分函数扩展了底函数。注意到这里有一个ln(x),我们可以把它移到方程的另一边。
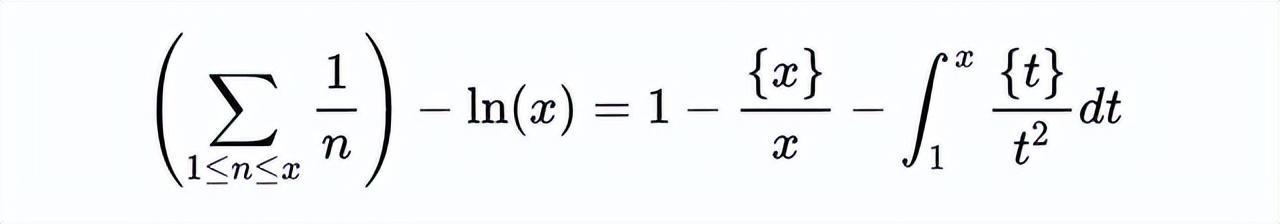
取x在两边趋于无穷时的极限,得到一个有趣的结果:

其中γ≈0.5772…为欧拉-马斯克若尼常数(调和级数与自然对数之间的极限差,我们在黎曼猜想系列文章中讲过)。欧拉-马斯克罗尼常数充满了神秘,我们对它一无所知(尚未被证明是代数的或超越的,甚至不知道γ是否是无理数),尽管它在数论和分析中随处可见。
我不知道你在想什么。至少我在想,如果我们可以用两个被积因子{t}和1/t来做偏积分不是很好吗?
不连续函数的不定积分
函数f的不定积分是一个可微函数F,它的导数等于原函数f,因此,不连续函数的不定积分是不存在的,因为它是不可微的。首先,回顾一下不定积分的特征是什么以及它们在分部积分法中的作用。
实际上,我们不需要假设积分因子是连续的,只需要假设它是勒贝格可积的。如果我们能找到一个函数f,它几乎在所有点上都是不定积分,这样就得到了f图下的面积,我们可以用通常的方法来做分部积分。
让我们仔细看看,如何找到函数f(t) = {t}从0到x的图下的面积公式,其中x是某个实数。有两种主要的思考方式。在这种情况下,最简单的方法是几何推导公式,因为当我们看{t}的图形时,很明显,面积将是面积为1/2的三角形的面积之和。
剩下的部分显然是1/2 {x},所以我们的公式是:
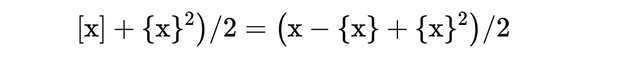
然而,我们将采用另一种方法,因为我想向你们展示一种更普遍的推导方法,因为将来我们可能必须找到{t}^2的积分,这在几何上不是那么容易。
利用在区间[n-1, n]上,有{t} = t - (n -1)这一事实。因此,我们可以将积分分解为具有整数端点的单元区间。具体地说:
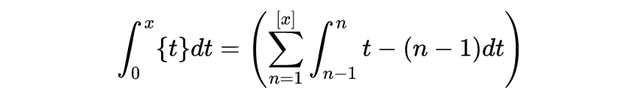
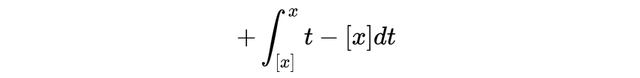
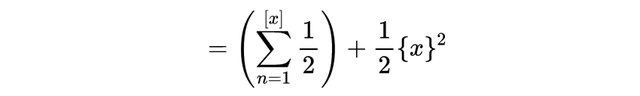
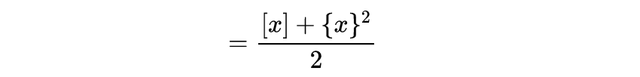
一般来说,我们可以通过在积分中使用替换来计算小数部分的n次幂:
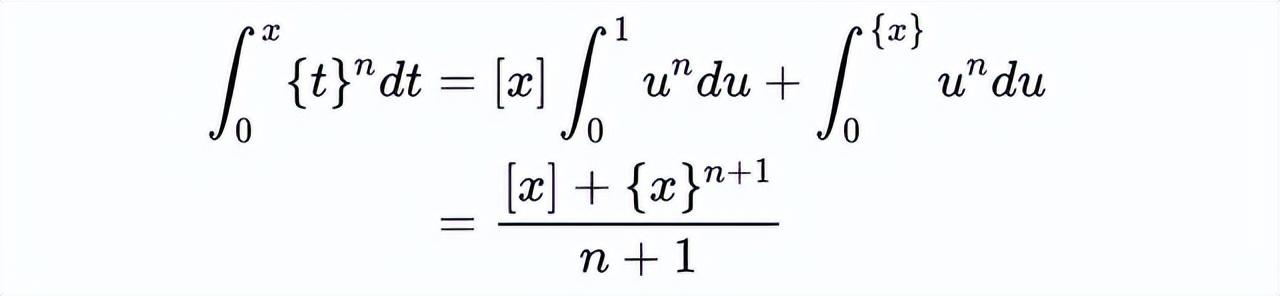
使用这种方法,我们可以对底函数做同样的计算。这里我将陈述两个需要解释的结果。但首先,让我说明一下:
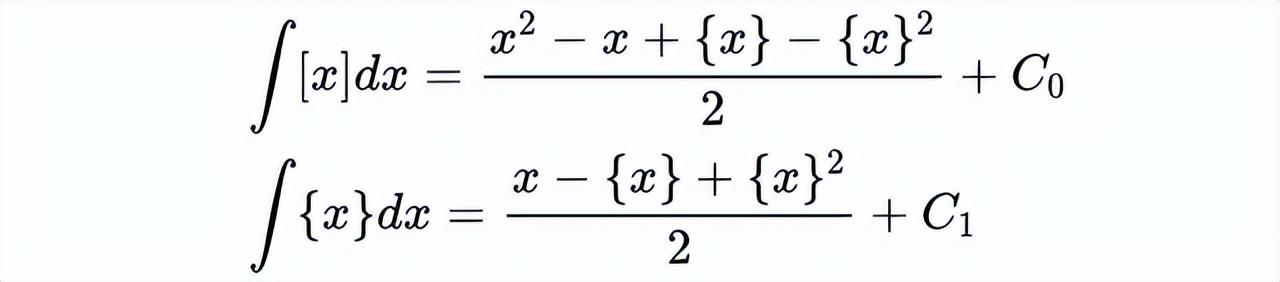
对于一些实数C_0和C_1。
这是什么意思呢?显然,这些函数是不可微的,所以它们不能是经典意义上的不定积分,因此我们可以说这是对符号的“滥用”,但是这个符号会有意义的,请耐心听我说。
以下是我的一些观察:
- 这些都是实际的面积函数,在某种意义上,如果让积分确定(从a到b的积分),用通常的方法把这些函数用作不定积分,然后我们得到两个图下的面积,这两个图的面积通常是x轴上和x轴下的面积之差。
- 分数部分函数和底函数仅在一组离散的点(即整数)上不可微。因此,它们实际上几乎在任何地方都是可微的,因为微分是一种局部(逐点))运算,我们可以表述如下:
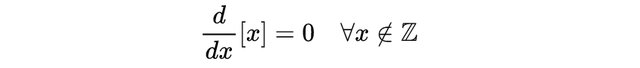
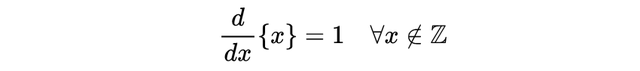
需要注意一点,微积分基本定理是不成立的。如果我们想要这样的东西,必须使用无穷级数的狄拉克函数,但我们并不需要它。
但上述观点仍然是正确的。因此我们可以用它来做分部积分。请注意,所有这些都完美地结合在了一起:
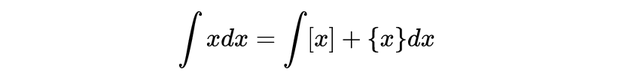
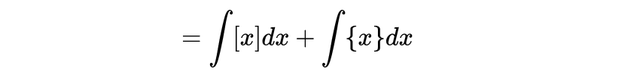
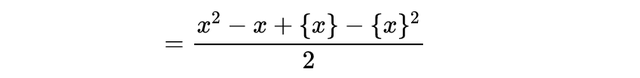
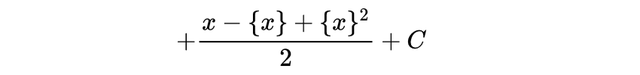
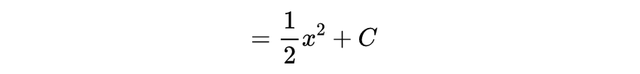
回顾欧拉常数
现在我们有了一些工具,我们该如何应用它们呢?
我们推导出了欧拉-马斯切罗尼常数的公式,现在我们拥有了足够强大的武器,可以进一步进行计算:
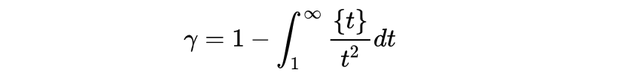

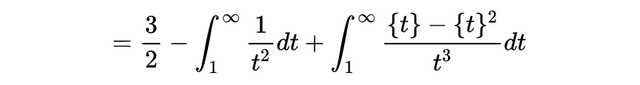

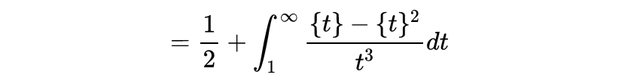
其中我们使用了分部积分法和关于{x}的积分公式。我们可以用部分积分来进一步接近γ。
数值分析
为了满足我自己的好奇心,我用Python做了一些数值积分。让我们创建一个用于数值积分的模块:







在一个单独的文件中,我们进行实际计算。我们从上面的模块中导入integral类,并定义分数部分函数和被积函数。



我们得到的数值大约是0.5772154,而真实值的开头部分为0.5772156649,精度还可以。如果提高精度或上限,会得到一个更好的近似,运行时间也会增加。
在数值方法中,这总是一种权衡。当然,没有什么比纯数学更好的了。




